Illustrationsbox Pareto-Analyse
Das Pareto-Prinzip wird auch 80/20-Regel bezeichnet und besagt, dass 80 % aller Wirkungen auf 20 % der möglichen Ursachen zurückzuführen sind. Im Kontext bestimmter Management-Methoden findet es in einem weiten Bereich der Kontrolle und Steuerung Anwendung. Das Pareto-Prinzip signalisiert ähnlich wie die ABC-Analyse Indikatoren, nach denen ineffiziente Teilmengen von Aktivitäten absortiert werden. Weist die ABC-Analyse mit der Klasse „A“ noch eine positive Teilmenge auf, die sich zu erweitern lohnt, bezieht sich das Pareto-Prinzip auf den oberen Teil der Menge, die Klasse „C“.
Hierfür liefert die Pareto-Analyse mit 80 % eine quantifizierte Größe, während die ABC-Analyse die Klassenbildung dem Betrachter überlässt. Im Rahmen der Pareto-Analyse lassen sich im Web-Business eine Reihe von Selektionen vornehmen, von den Kundengruppen, den Gütern, zu der Wirksamkeit von Werbemaßnahmen, der Effizienz von Bannern bis hin zu der Auswahl von Methoden der Usability oder der Gewinnsteigerung.
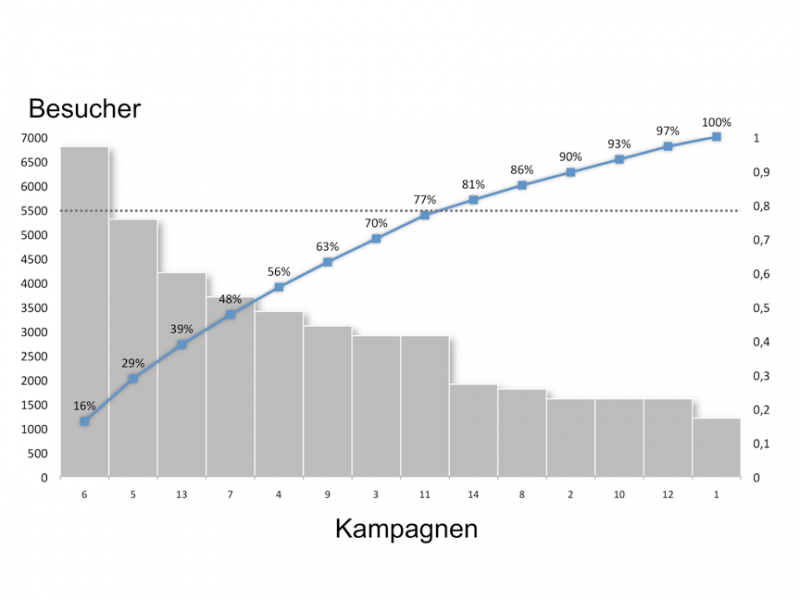
Anhand des folgenden Beispiels werden die Kampagnen eines Werbekontos (AdWords) aus Tabelle 4. .3-1: Kosten der Anzeigenwerbung in eine Pareto Grafik übertragen.
Abbildung Pareto-Analyse
Das Ergebnis der Pareto-Analyse weist darauf hin, dass die ersten acht Kampagnen mehr als 80 % der Besucher mit den AdWords-Kampagnen einholen. Die restlichen sechs Kampagnen tragen weniger als 20 % zu dem Besuchervolumen bei. Diese Analyse sagt nichts über die Effizienz oder den Gewinnbeitrag der einzelnen Kampagnen aus.
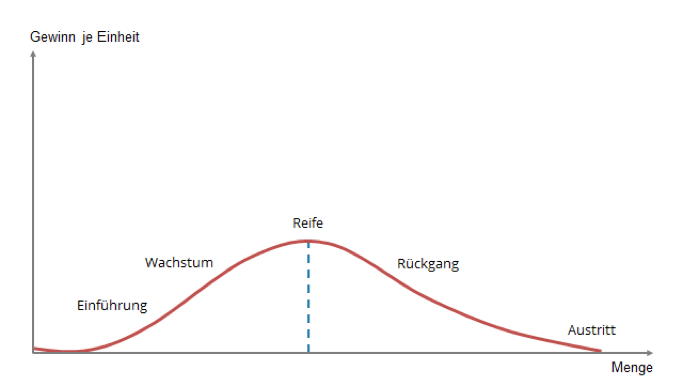
Illustrationsbox Lebenszyklus der Potenzialnutzung
Der Wendepunkt der logistischen Funktion des Potenzials entspricht dem Zenit einer Glockenkurve, da die Steigung am Wendepunkt ihren höchsten Wert erreicht und anschließend abnimmt. Die Glockenkurve bestimmt eine ökonomische Interpretation, sie wird als Lebenszyklus der Güter verstanden, der analog zur Wertschöpfung verlaufen soll. Die Glockenkurve bezeichnet die erste Ableitung der Sättigungskurve:
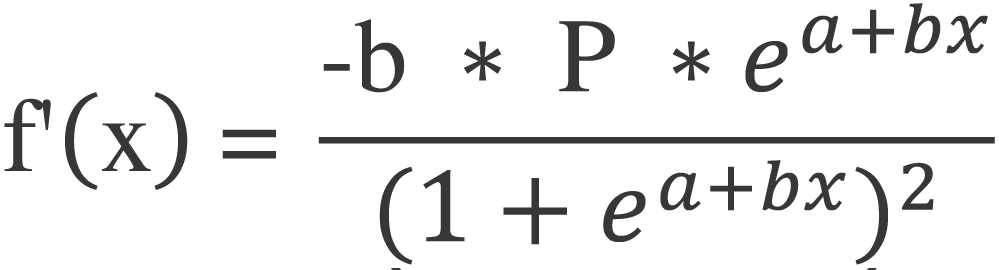
Mit P = Potenzial, b = Steigung, a = b * ()[1]
In ökonomischen Zusammenhängen erhält die erste Ableitung das Präfix „Grenz-“, wodurch die Begriffe „Grenzkosten“, „Grenzertrag“ und “Grenznutzen“ entstehen. Der Grenzgewinn ist die Steigerung des Gewinns an der Grenze:
![]()
Mit G`= Grenzgewinn, G = Gewinn, B = Besucher
In ihrer allgemeinen Form lassen die Grenzwerte eine Orientierung zu, an welcher Position das Unternehmen in der Nutzung oder Entwicklung seiner Potenziale steht.
Abbildung Lebenszyklus der Güter
In Anwendung dieser theoretischen Überlegungen auf das Web-Business finden sich Entscheidungshilfen zu der Ausweitung einer Strategie in dem bestehenden Potenzial oder der Suche nach neuen Potenzialen. Beispielsweise lässt sich prüfen, ob eine Website weiterhin für die Suchmaschinen optimiert wird oder der Kauf von qualifizierten Besuchern aus der Zielgruppe vorangetrieben wird. Beide Marketingvarianten haben ihre eigene Sättigungskurve in ihrem Potenzial, der Webmaster steht vor der Entscheidung, in welches Potenzial er weiteren Aufwand investiert. Die Ergebnisse und freien Potenziale werden ganz unterschiedlich sein, je nachdem, an welchem Punkt der Sättigungskurve jede Variante steht.
[1] Die Formulierung zur ersten Ableitung der Wachstumsfunktion in Potenzialen ist analog zu Schwarze (vgl. Schwarze 2000: 58 ff.).
Illustrationsbox Potenzialkurve
In der virtuellen Ökonomie trifft das Unternehmen auf neue Märkte, neue Zielgruppen, Wettbewerber und Chancen. Es gilt, neue Potenziale zu erschließen, und diese Aufgabe lässt sich nicht ohne Weiteres mit den etablierten Methoden der Ökonomik lösen, weil die konventionelle Ökonomie unter den Annahmen eines vollständigen Wettbewerbs, vollständiger Information und preisabhängiger Entscheidungen agiert.
Im Web-Business ist die Exponentialfunktion zur Ausschöpfung des Potenzials (P) eine adäquate Modellierung der Randbedingungen:
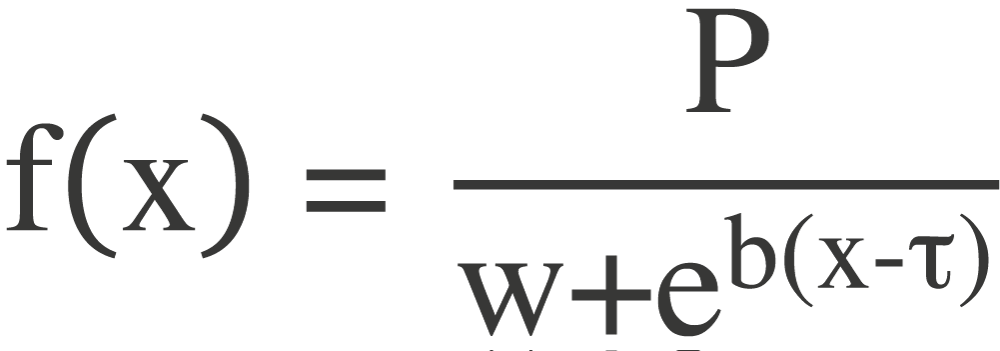
Mit P = Potenzial, t = Wendepunkt, b = Steigung, w = Normierungsgröße (Wettbewerber), x = Ereignisse
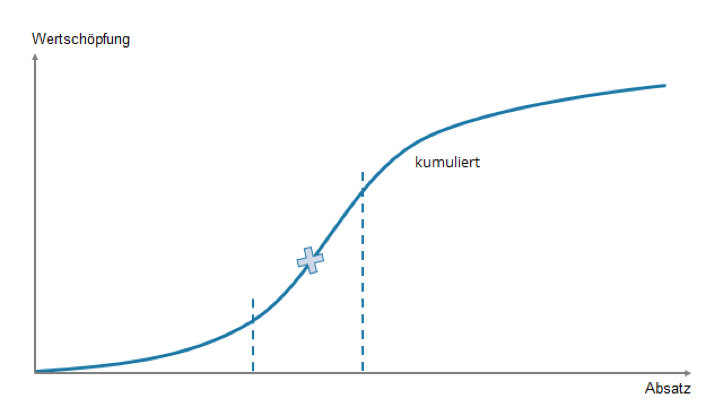
Sie hat die grafische Visualisierung einer S-Kurve: In der Ökonomie wird meist die Region um den Wendepunkt der Sättigungskurve betrachtet; dort ist unter Rentabilitätsgesichtspunkten die interessanteste Region. Die Aktivitäten tragen deutlich zur Nutzung der Potenziale des Unternehmens bei, sie generieren Ergebnisse, die zu den Ursachen (Aktionen) in einer normierten Relation stehen und nach ihrer Effizienz unterschiedlich geschichtet sind.
Abbildung Potenzialkurve in der Ökonomie
Diese Entwicklungslinie beginnt vor dem Wendepunkt der logistischen Sättigungskurve. In der konventionellen Ökonomie wird hauptsächlich dieser Teil der Potenzialkurve verwendet. Bei der Nutzung von Ressourcen lehnt er sich an das zweite Goossen’sche „Gesetz“ an. Dieses besagt, dass der Nutzen eines Gutes mit der Menge des Konsums abnimmt. Die Entsprechung auf der Unternehmensseite fokussiert die Entwicklung der gesamten Wertschöpfung aus einer Ressource, einem Teilmarkt, einer Kundengruppe oder einem Marktpotenzial eines Gutes. Um die Position auf der Potenzialkurve des Ertrages oder der Wertschöpfung genauer zu bestimmen, wird der sogenannte „Grenzertrag“ als Steigerung ermittelt. Der Grenzertrag bestimmt die erste Ableitung der Sättigungskurve des Ertrags.
Illustrationsbox Kostenminimierung im Web-Business
Das strategische Ziel lautet: Minimiere die (variablen) Kosten unter Nutzung des Webs als Rahmenbedingung (oder Potenzial) und wird formal geschrieben zu:
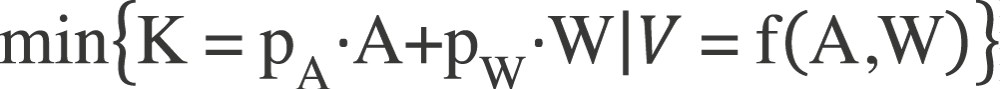
mit K = Kosten, A = Arbeit, W = Wissen (Information) und V = Virtuelles Gut Die Nebenbedingung sei eine einfache neoklassische Produktionsfunktion:
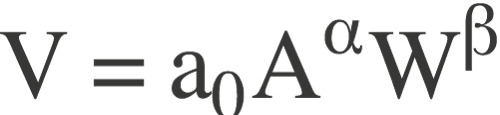
mit α und β als partielle Produktionselastizitäten (oder einfach als Produktivität) der Inputfaktoren Arbeit und Wissen. Für eine homogene Produktionsfunktion ist die Skalenelastizität (α+ β) = 1 und beschreibt das lineare Wachstum ohne Skaleneffekte.
Die Produktionsfunktion wurde in der Illustrationsbox 3.2 besprochen. Sie gibt die Auswahlmöglichkeiten oder das Potenzial an. Jetzt wird sie mit den Kosten der Einsatzfaktoren verbunden zu dem Optimierungsziel unter allen möglichen Varianten die kostengünstigste zu finden.